My research interests lie in optimization, control, and learning of dynamical systems. I am curious about the interaction between the physical world and computing pipelines.
Decision Dependence
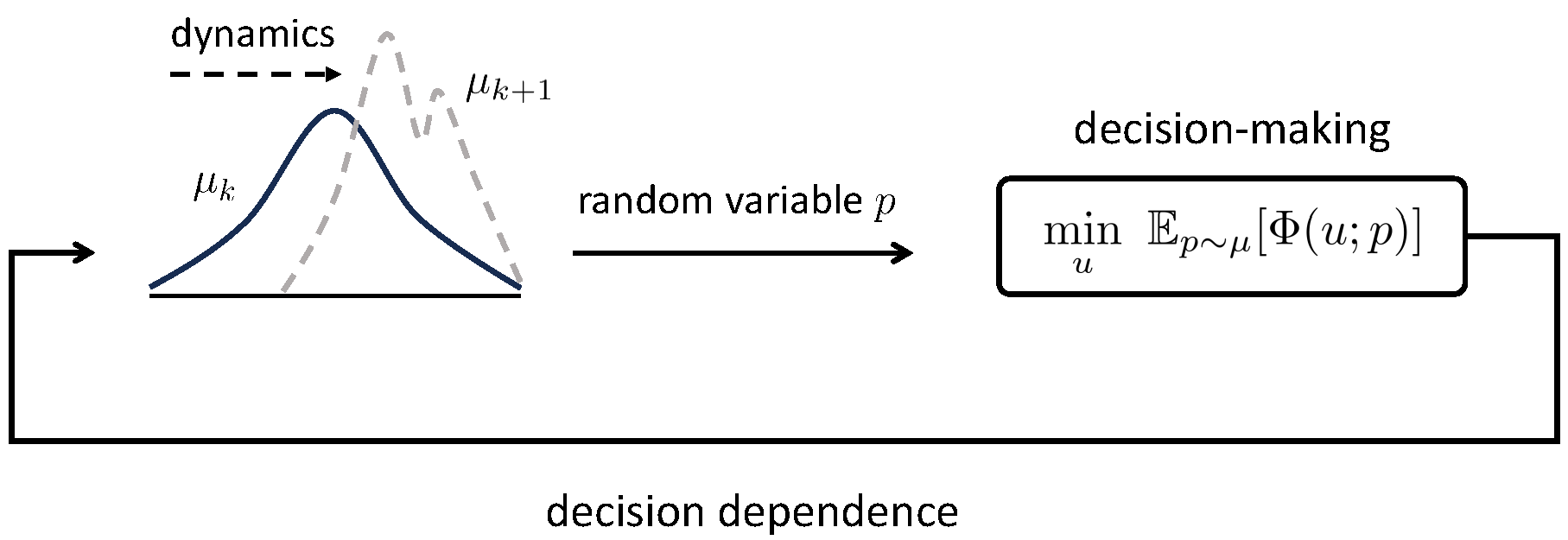
Distribution shifts are often deemed as undesirable external forces that a decision maker should counteract (e.g., via out-of-distribution detection) or conform to (e.g., via online learning or distributionally robust optimization). A feedback phenomenon arises, however, when the deployed decision affects the data-generating distribution. In this regard, performative prediction encodes such a dependence as a static parameterized map.
In contrast, I and my collaborators formulate distribution shifts as feedback processes equipped with nonlinear dynamics and driven by a decision maker. This perspective of distribution dynamics motivates us to leverage the composite problem structure and shape future distributions via anticipating sensitivities, thereby enabling optimal decision-making.
Optimization Algorithms as Feedback Controllers
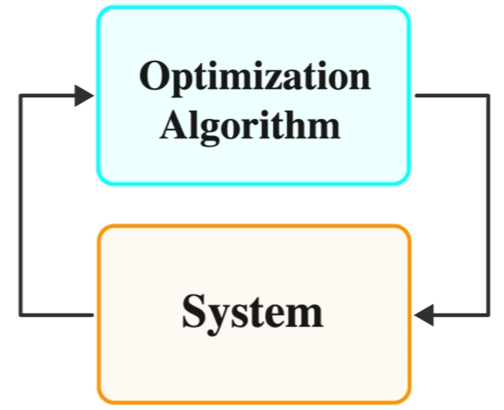
Optimal steady-state operation of an engineering system is critical. To this end, traditional numerical optimization relies on an exact problem formulation that encompasses system models and disturbance statistics. Such a feedforward pipeline, however, can be restrictive and suboptimal when accurate information on models and disturbances is unavailable.
In contrast, the emerging paradigm of feedback optimization bypasses such information and fulfills autonomous optimality-seeking in closed loop. Along this line, we develop fully model-free methods that avoids accessing any model information by exploiting real-time evaluations of objective functions.
Interestingly, model-based and model-free methods own complementary benefits in sample efficiency and provable accuracy. We further propose gray-box methods that incorporate prior approximate knowledge to achieve the best of both worlds.
Approximation-Enabled Distributed Optimization
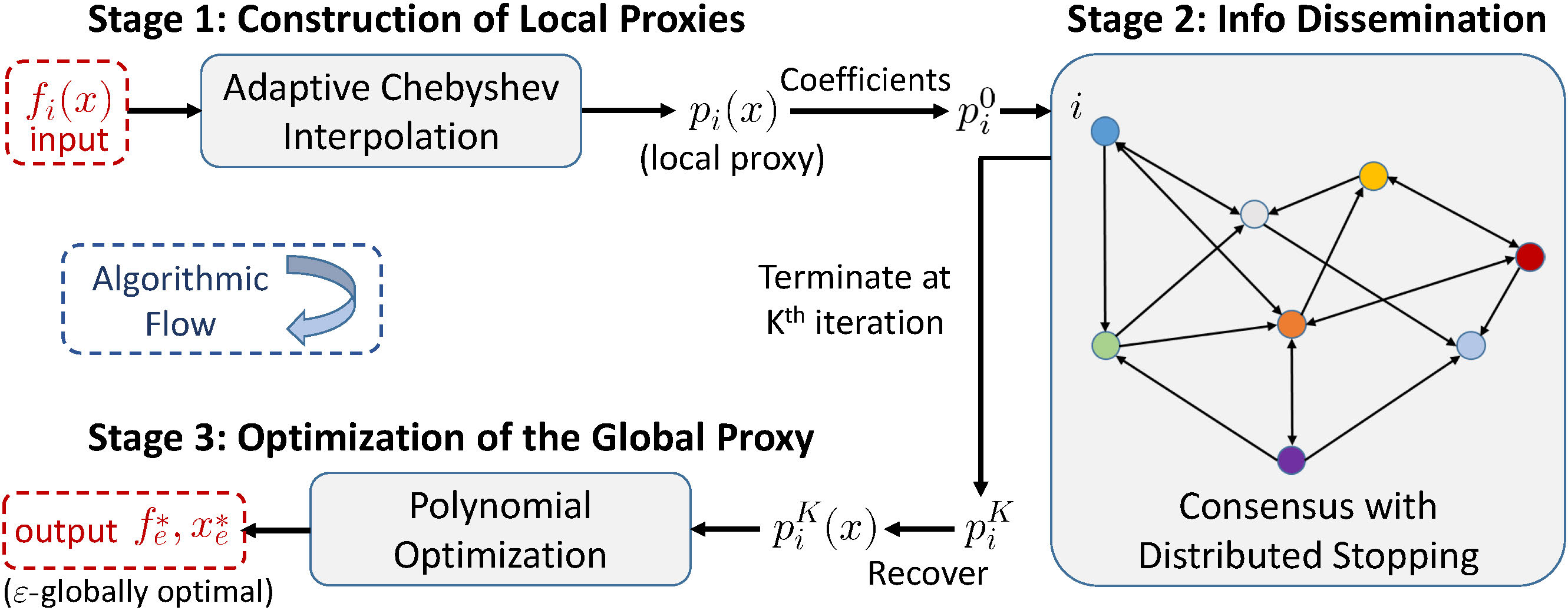
Distributed optimization is one of the cornerstones of scalable and robust decision-making in the era of large-scale network systems. While numerous distributed gradient-based algorithms have been developed, they generally suffer from a growing cost of querying gradients, function values, or Hessians with respect to the number of iterations. Moreover, it is prohibitive to guarantee global optimality for nonconvex problems.
In contrast, we attack distributed optimization from a unique perspective of function approximation. The key insight is to leverage polynomial approximation as a surrogate representation of the local objective function. This representation facilitates smooth information dissemination over networks and promises tractable reformulations for global optimization. Our approximation-enabled algorithms feature arbitrarily precise global optimization, fixed costs of function evaluations, and provable guarantees on data privacy and robustness.
Engineering Applications
Modern engineering systems are inherently complex, consisting of multiple interacting layers and components and operating under changing conditions. Our aforementioned contributions feature data-driven workflows, minimal model information, and efficient adaptation, and are well suited for addressing practical challenges arising from those complex engineering systems.
Together with my excellent collaborators and students (see my teaching page), we explore the following questions in the domains of power grids and transportation systems:
- voltage control in the face of volatile renewable generation;
- online dynamic pricing in electrical distribution systems;
- distributed and hierarchical decision-making in mobility systems.